Pythonで購入履歴の共起分析による推薦システム開発

2022-06-04

software

商品購入ログを使って商品の推薦システムを作る

商品購入ログから商品の推薦を行う。
「この商品を買った人はこれも買ってます」というやつ。

これは共起分析によって簡単に実現できる。
共起分析とは「共に起こる」の通り、同時に発生したかどうかを特徴として分析する手法。

具体的に今回の購入ログの例でいうと、
「あるユーザーが商品Aと商品Bを両方購入している」とか、
「ある商品をユーザーAとユーザーBが両方購入している」とか、
そういった情報を特徴として分析に使用する。

これによってある商品を買った人が一緒に何を買いがちか分かる、
この結果を任意の商品を買ったユーザーに伝えることで他の商品を推薦できる。
今回はPythonで実験する。

• 1. 環境構築
• 2. 使用データ
• 3. 実験
  • 3.1. クロス集計
  • 3.2. 共起分析　出現アイテムの組み合わせ作成
  • 3.3. 共起分析　集合の類似度計算
  • 3.5. 結果
• 4. コード

1. 環境構築

Anacondaが既にインストールされている前提。
入ってなければ以下を参考にして入れる。

Anacondaのインストール

Anacondaのインストールこのブログ内でよく「Anacondaがインストールされている想定」と書くが一度もインストールの方法を書いていないのでここに書く。非…

以下のように「data」という名前の環境を作り、必要なライブラリをインストール。

1 2 3

conda create -n data python=3.9 conda activate data conda install -c anaconda pandas

終わり。

2. 使用データ

手元にあった下記の購入履歴を使用。
ストラクチャーデッキを参考にしている。

yugioh_log.csv

時刻	購入者	商品
0:19:15	城之内	クリッター
1:16:21	遊戯	ブラック・マジシャン・ガール
2:06:38	海馬	融合
2:34:36	遊戯	ブラック・マジシャン
2:57:13	海馬	融合解除
4:04:33	マリク	サイクロン
4:38:45	パンドラ	死のマジック・ボックス
4:48:40	海馬	リビングデッドの呼び声
5:18:28	城之内	ハリケーン
6:33:19	遊戯	死者蘇生
8:46:46	遊戯	融合
9:40:23	遊戯	ブラック・ホール
9:40:30	ペガサス	死者蘇生
10:26:40	ペガサス	融合
10:54:43	ペガサス	大嵐
11:33:02	ペガサス	ハリケーン
14:19:39	マリク	聖なるバリア −ミラーフォース−
15:44:19	海馬	ブラック・ホール
15:44:37	城之内	融合
16:29:03	ペガサス	クリッター
17:05:46	マリク	死者蘇生
17:09:09	海馬	死者蘇生
20:26:48	城之内	リビングデッドの呼び声
21:13:05	海馬	青眼の白龍
21:41:42	城之内	サイクロン
21:49:30	ペガサス	融合解除
21:52:27	遊戯	聖なるバリア −ミラーフォース−
21:59:26	マリク	融合
22:15:42	パンドラ	ブラック・マジシャン
23:14:51	遊戯	融合解除
23:17:19	遊戯	サイクロン
23:23:05	遊戯	クリッター
23:55:36	海馬	クリッター
23:56:50	遊戯	死のマジック・ボックス
23:55:56	海馬	青眼の白龍

3. 実験

さっきの購入履歴を使用してPythonによって実験。

3.1. クロス集計

はじめにpandasによってデータを取得。
その後pandasの関数で「商品」と「購入者」のクロス集計を行う。

クロス集計とは、今回の例でいうと「商品」を縦軸、「購入者」を横軸として、
各商品の行に対して、それを購入した人の列に「購入した数」が与えられる集計方法。

今回は購入したかどうかだけを見るためにcross = cross.mask(cross > 0, 1)として、「1以上」を全部「1」にしている。
これをしないと特定のひとりが大量に何かを買った時にノイズになる(かもしれない)。

1 2 3 4 5 6 7 8

import pandas as pd #### CSV読み込み loadcsv = "yugioh_log.csv" df = pd.read_csv(loadcsv, encoding="shift-jis") # ← CSVの文字コードがutf8なら encoding="utf-8" #### クロス集計 cross = pd.crosstab(df["商品"], df["購入者"])

こんな感じになる↓

商品	パンドラ	ペガサス	マリク	城之内	海馬	遊戯
クリッター	0	1	0	1	1	1
サイクロン	0	0	1	1	0	1
ハリケーン	0	1	0	1	0	0
ブラック・ホール	0	0	0	0	1	1
ブラック・マジシャン	1	0	0	0	0	1
ブラック・マジシャン・ガール	0	0	0	0	0	1
リビングデッドの呼び声	0	0	0	1	1	0
大嵐	0	1	0	0	0	0
死のマジック・ボックス	1	0	0	0	0	1
死者蘇生	0	1	1	0	1	1
聖なるバリア −ミラーフォース−	0	0	1	0	0	1
融合	0	1	1	1	1	1
融合解除	0	1	0	0	1	1
青眼の白龍	0	0	0	0	1	0

3.2. 共起分析　出現アイテムの組み合わせ作成

さっきのクロス集計した表を使用して共起分析。
itertoolsで組み合わせ作成。
collectionsで出現回数取得。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

#### 共起分析 import itertools import collections import csv # 各ユーザーごとに購入した商品の組み合わせを作成 word_lists = [] # 購入者毎の購入商品リスト combi_lists = [] # 購入者毎の購入商品の組み合わせリスト for column_name in cross: # 購入者 毎にループ # 出現回数１回以上の商品をリスト化 ⇒ 2種類ずつ全通りの組み合わせを作成 word_list = cross.index[cross[column_name] >= 1].tolist() combi_list = list(itertools.combinations(word_list,2)) word_lists.extend(word_list) combi_lists.extend(combi_list) # word_counters：「購入商品」と「出現回数」 # combi_counters：「購入商品の組み合わせ」と「出現回数」 word_counters = collections.Counter(word_lists) combi_counters = collections.Counter(combi_lists)

3.3. 共起分析　集合の類似度計算

ユーザー全体に対して商品Aを購入したユーザーを集合A、
商品Bを購入したユーザーを集合Bとする。
その場合、商品Aと商品Bを両方購入したユーザーは集合Aと集合Bの積集合となる。

---

---

このとき、たとえば集合A、集合B、の大きさが10で積集合ABの大きさが9だったら集合Aと集合Bの内容はほぼ一致していることが分かる。

---

---

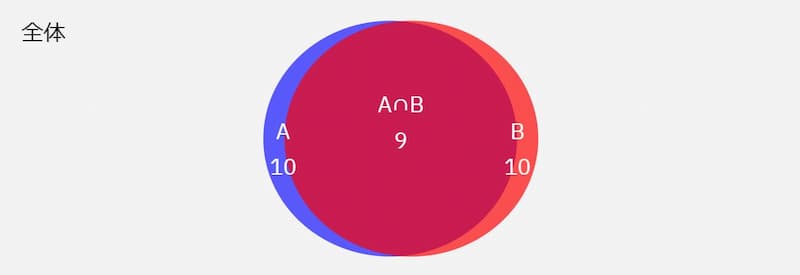
逆に、集合A、集合B、の大きさが10で積集合ABの大きさが1だったら集合Aと集合Bの内容はほぼ異なっていることが分かる。

---

---

このようにして、集合同士の類似度は計算によって定量評価することができる。
今回はJaccard係数、Dice係数、Simpson係数の3つの指標によって類似度の計算を行う。

各係数の計算式はコード内のコメント参照。

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

# 集合の類似度計算 output_list = [] # csv出力用 for combi in combi_counters: # 商品Aと商品Bの組み合わせ全パターンに対して共通度を計算 A_B_seki = combi_counters[combi] # A∩B A_set = word_counters[combi[0]] # A B_set = word_counters[combi[1]] # B A_B_wa = A_set + B_set - A_B_seki # AUB = A + B - A∩B Jaccard = A_B_seki / A_B_wa # Jaccard = A∩B / AUB Dice = 2 * A_B_seki / (A_set + B_set) # Dice = 2|A∩B| / A + B Simpson = A_B_seki / min(A_set, B_set) # Simpson = A∩B / min(A + B) # CSV出力用 output_list.append([combi[0], combi[1], A_set, B_set, A_B_seki, A_B_wa, Jaccard, Dice, Simpson]) output_list.append([combi[1], combi[0], B_set, A_set, A_B_seki, A_B_wa, Jaccard, Dice, Simpson]) # 逆順も出力 # csv出力 with open("yugioh_log_kyoki.csv", "w", newline="") as f: writer = csv.writer(f) writer.writerow(["商品A", "商品B", "A購入ユーザー数", "B購入ユーザー数", "A∩B", "AUB", "Jaccard", "Dice", "Simpson"]) writer.writerows(output_list)

こんな感じになる(一部抜粋)↓

商品A	商品B	A購入ユーザー数	B購入ユーザー数	A∩B	AUB	Jaccard	Dice	Simpson
ブラック・マジシャン	死のマジック・ボックス	2	2	2	2	1	1	1
死のマジック・ボックス	ブラック・マジシャン	2	2	2	2	1	1	1
クリッター	ハリケーン	4	2	2	4	0.5	0.6666666667	1
ハリケーン	クリッター	2	4	2	4	0.5	0.6666666667	1
クリッター	大嵐	4	1	1	4	0.25	0.4	1
大嵐	クリッター	1	4	1	4	0.25	0.4	1
クリッター	死者蘇生	4	4	3	5	0.6	0.75	0.75
死者蘇生	クリッター	4	4	3	5	0.6	0.75	0.75
クリッター	融合	4	5	4	5	0.8	0.8888888889	1
融合	クリッター	5	4	4	5	0.8	0.8888888889	1
クリッター	融合解除	4	3	3	4	0.75	0.8571428571	1
融合解除	クリッター	3	4	3	4	0.75	0.8571428571	1
ハリケーン	大嵐	2	1	1	2	0.5	0.6666666667	1
大嵐	ハリケーン	1	2	1	2	0.5	0.6666666667	1
ハリケーン	死者蘇生	2	4	1	5	0.2	0.3333333333	0.5
死者蘇生	ハリケーン	4	2	1	5	0.2	0.3333333333	0.5
ハリケーン	融合	2	5	2	5	0.4	0.5714285714	1
融合	ハリケーン	5	2	2	5	0.4	0.5714285714	1
ハリケーン	融合解除	2	3	1	4	0.25	0.4	0.5
融合解除	ハリケーン	3	2	1	4	0.25	0.4	0.5

このデータを使用するとある商品と類似度の高い商品が分かる。
たとえば「ブラックマジシャン」についてJaccard係数の高い順に並び変えると以下のようになる。

商品A	商品B	Jaccard
ブラック・マジシャン	死のマジック・ボックス	1
ブラック・マジシャン	ブラック・マジシャン・ガール	0.5
ブラック・マジシャン	ブラック・ホール	0.3333333333
ブラック・マジシャン	聖なるバリア −ミラーフォース−	0.3333333333
ブラック・マジシャン	サイクロン	0.25
ブラック・マジシャン	融合解除	0.25
ブラック・マジシャン	クリッター	0.2
ブラック・マジシャン	死者蘇生	0.2
ブラック・マジシャン	融合	0.1666666667

3.5. 結果

計算式の都合上、Jaccard係数は2つの集合の大きさに差があると値が極端に小さくなる。
分母が和集合なのに対して、分子が積集合(小さいほうの集合の大きさが大きさの最大値)であるため。

Simpson係数は分母を2集合の大きさの最小値としているため上記の問題は解決されているが、片方の集合がもう片方の集合に完全に含まれる場合に値が1となる。
これにより出現回数が極端に少ないアイテムがたまたまSimpson係数1となり類似度の上位に位置する問題がある。

Dice係数は両者の中間になるように思えるがかなりJaccard寄り。
Jaccard係数の結果とほぼ変わらない。

いずれにせよ集合の大きさが小さいアイテムは削除するなど工夫が必要。

4. コード

全部まとまった状態のコード

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47

import pandas as pd import itertools import collections import csv #### CSV読み込み loadcsv = "yugioh_log.csv" df = pd.read_csv(loadcsv, encoding="shift-jis") # ← CSVの文字コードがutf8なら encoding="utf-8" #### クロス集計 cross = pd.crosstab(df["商品"], df["購入者"]) #### 共起分析 # 各ユーザーごとに購入した商品の組み合わせを作成 word_lists = [] # 購入者毎の購入商品リスト combi_lists = [] # 購入者毎の購入商品の組み合わせリスト for column_name in cross: # 購入者 毎にループ # 出現回数１回以上の商品をリスト化 ⇒ 2種類ずつ全通りの組み合わせを作成 word_list = cross.index[cross[column_name] >= 1].tolist() combi_list = list(itertools.combinations(word_list,2)) word_lists.extend(word_list) combi_lists.extend(combi_list) # word_counters：「購入商品」と「出現回数」 # combi_counters：「購入商品の組み合わせ」と「出現回数」 word_counters = collections.Counter(word_lists) combi_counters = collections.Counter(combi_lists) # 集合の類似度計算 output_list = [] # csv出力用 for combi in combi_counters: # 商品Aと商品Bの組み合わせ全パターンに対して共通度を計算 A_B_seki = combi_counters[combi] # A∩B A_set = word_counters[combi[0]] # A B_set = word_counters[combi[1]] # B A_B_wa = A_set + B_set - A_B_seki # AUB = A + B - A∩B Jaccard = A_B_seki / A_B_wa # Jaccard = A∩B / AUB Dice = 2 * A_B_seki / (A_set + B_set) # Dice = 2|A∩B| / A + B Simpson = A_B_seki / min(A_set, B_set) # Simpson = A∩B / min(A + B) # CSV出力用 output_list.append([combi[0], combi[1], A_set, B_set, A_B_seki, A_B_wa, Jaccard, Dice, Simpson]) output_list.append([combi[1], combi[0], B_set, A_set, A_B_seki, A_B_wa, Jaccard, Dice, Simpson]) # 逆順も出力 # csv出力 with open("yugioh_log_kyoki.csv", "w", newline="") as f: writer = csv.writer(f) writer.writerow(["商品A", "商品B", "A購入ユーザー数", "B購入ユーザー数", "A∩B", "AUB", "Jaccard", "Dice", "Simpson"]) writer.writerows(output_list)

タグ Machine Learning, Python, pandas, scikit-learn