Pythonで購入履歴の共起分析(アイテム間類似度取得・クラスタリング)

2022-06-09

商品購入ログから商品間の類似度取得・クラスタリング

商品購入ログを使って商品の共起分析。
以前行った実験と同じデータを使ってより高度な前処理を行う。

前回の実験↓

Pythonで購入履歴から商品のクラスタリング(3パターン)

商品購入ログを使って商品のクラスタリング商品購入ログから商品のクラスタリングをしたい。Pythonの最強ライブラリscikit-learnを使って行う。最もメジ…

Pythonで購入履歴の共起分析による推薦システム開発

今回は下記の図に示すようにデータを加工していく。

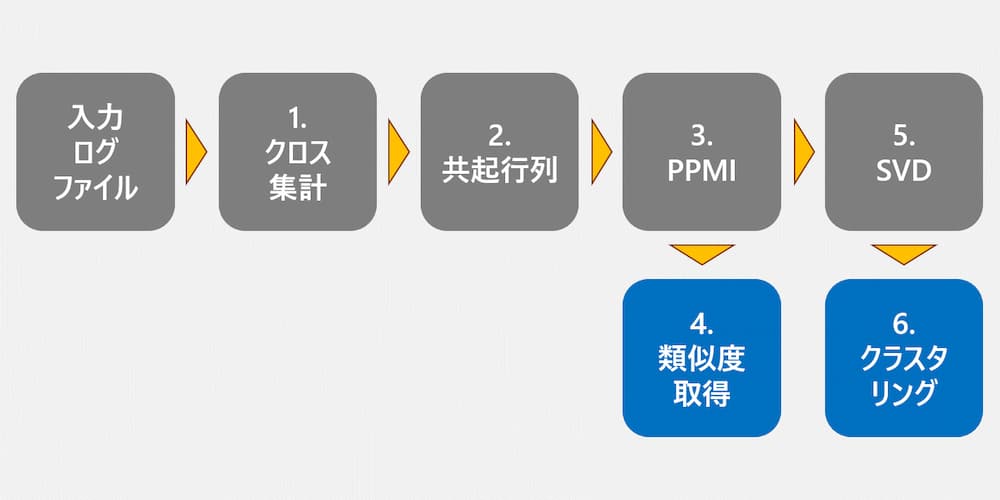
ログデータのクロス集計までは前回と一緒。

その後、

共起行列
PPMI
SVD

と続く。

成果物として、

アイテム間のコサイン類似度表
アイテムのクラスタリングリスト

が得られる。

1. 環境構築
2. 使用データ
3. 実験
4. コード
5. 参考

1. 環境構築

Anacondaが既にインストールされている前提。
入ってなければ以下を参考にして入れる。

Anacondaのインストール

Anacondaのインストールこのブログ内でよく「Anacondaがインストールされている想定」と書くが一度もインストールの方法を書いていないのでここに書く。非…

以下のように「data」という名前の環境を作り、必要なライブラリをインストール。

conda create -n data python=3.9
conda activate data
conda install -c anaconda pandas
conda install -c conda-forge matplotlib
conda install -c anaconda scikit-learn

終わり。

2. 使用データ

手元にあった下記の購入履歴を使用。
ストラクチャーデッキを参考にしている。

yugioh_log.csv

時刻	購入者	商品
0:19:15	城之内	クリッター
1:16:21	遊戯	ブラック・マジシャン・ガール
2:06:38	海馬	融合
2:34:36	遊戯	ブラック・マジシャン
2:57:13	海馬	融合解除
4:04:33	マリク	サイクロン
4:38:45	パンドラ	死のマジック・ボックス
4:48:40	海馬	リビングデッドの呼び声
5:18:28	城之内	ハリケーン
6:33:19	遊戯	死者蘇生
8:46:46	遊戯	融合
9:40:23	遊戯	ブラック・ホール
9:40:30	ペガサス	死者蘇生
10:26:40	ペガサス	融合
10:54:43	ペガサス	大嵐
11:33:02	ペガサス	ハリケーン
14:19:39	マリク	聖なるバリア −ミラーフォース−
15:44:19	海馬	ブラック・ホール
15:44:37	城之内	融合
16:29:03	ペガサス	クリッター
17:05:46	マリク	死者蘇生
17:09:09	海馬	死者蘇生
20:26:48	城之内	リビングデッドの呼び声
21:13:05	海馬	青眼の白龍
21:41:42	城之内	サイクロン
21:49:30	ペガサス	融合解除
21:52:27	遊戯	聖なるバリア −ミラーフォース−
21:59:26	マリク	融合
22:15:42	パンドラ	ブラック・マジシャン
23:14:51	遊戯	融合解除
23:17:19	遊戯	サイクロン
23:23:05	遊戯	クリッター
23:55:36	海馬	クリッター
23:56:50	遊戯	死のマジック・ボックス
23:55:56	海馬	青眼の白龍

3. 実験

さっきの購入履歴を使用してPythonによって実験。

3.1. クロス集計

はじめにpandasによってデータを取得。
その後pandasの関数で「商品」と「購入者」のクロス集計を行う。

前回説明したのと同じなので割愛。

import pandas as pd

#### CSV読み込み
loadcsv = "yugioh_log.csv"
df = pd.read_csv(loadcsv, encoding="shift-jis") # ← CSVの文字コードがutf8なら encoding="utf-8"

#### 1. クロス集計
cross = pd.crosstab(df["商品"], df["購入者"])
cross = cross.mask(cross > 0, 1) # 2回以上でも1にする

こんな感じになる↓

商品	パンドラ	ペガサス	マリク	城之内	海馬	遊戯
クリッター	0	1	0	1	1	1
サイクロン	0	0	1	1	0	1
ハリケーン	0	1	0	1	0	0
ブラック・ホール	0	0	0	0	1	1
ブラック・マジシャン	1	0	0	0	0	1
ブラック・マジシャン・ガール	0	0	0	0	0	1
リビングデッドの呼び声	0	0	0	1	1	0
大嵐	0	1	0	0	0	0
死のマジック・ボックス	1	0	0	0	0	1
死者蘇生	0	1	1	0	1	1
聖なるバリア −ミラーフォース−	0	0	1	0	0	1
融合	0	1	1	1	1	1
融合解除	0	1	0	0	1	1
青眼の白龍	0	0	0	0	1	0

3.2. 共起行列　作成

さっきのクロス集計した表から共起行列を作成する。
共起行列について今回作成する具体例をもとに説明する。

さきほどのクロス集計では縦が「商品」、横が「ユーザー」となっていたところを、
縦、横ともに「商品」とする。

仮に縦を「商品A」、横を「商品B」とすると、【「商品A」行・「商品B」列】の値は、
クロス集計で「商品A」と「商品B」を両方購入したユーザーの数になる。

共起行列に変換することで(大抵の場合は)次元数が削減される。
今回のように商品数よりユーザー数の方が少ない場合は効果がないが、
大抵の場合はユーザー数の方がはるかに大きい。

クロス集計から共起行列への変換は、
「クロス集計」と「転置した自分自身」の内積をとることで簡単に取得できる。

1
2
3

#### 2. 共起行列
co_occurrence = cross.dot(cross.T)
co_occurrence.to_csv("yugioh_log_co_occurrence.csv", encoding="shift-jis")

こんな感じになる↓

商品	クリッター	サイクロン	ハリケーン	ブラック・ホール	ブラック・マジシャン	ブラック・マジシャン・ガール	リビングデッドの呼び声	大嵐	死のマジック・ボックス	死者蘇生	聖なるバリア－ミラーフォース－	融合	融合解除	青眼の白龍
クリッター	4	2	2	2	1	1	2	1	1	3	1	4	3	1
サイクロン	2	3	1	1	1	1	1	0	1	2	2	3	1	0
ハリケーン	2	1	2	0	0	0	1	1	0	1	0	2	1	0
ブラック・ホール	2	1	0	2	1	1	1	0	1	2	1	2	2	1
ブラック・マジシャン	1	1	0	1	2	1	0	0	2	1	1	1	1	0
ブラック・マジシャン・ガール	1	1	0	1	1	1	0	0	1	1	1	1	1	0
リビングデッドの呼び声	2	1	1	1	0	0	2	0	0	1	0	2	1	1
大嵐	1	0	1	0	0	0	0	1	0	1	0	1	1	0
死のマジック・ボックス	1	1	0	1	2	1	0	0	2	1	1	1	1	0
死者蘇生	3	2	1	2	1	1	1	1	1	4	2	4	3	1
聖なるバリア－ミラーフォース－	1	2	0	1	1	1	0	0	1	2	2	2	1	0
融合	4	3	2	2	1	1	2	1	1	4	2	5	3	1
融合解除	3	1	1	2	1	1	1	1	1	3	1	3	3	1
青眼の白龍	1	0	0	1	0	0	1	0	0	1	0	1	1	1

3.3. PPMI 計算

上記の表をそのまま分析に使うと単純に出現回数の多いアイテムがあらゆるものと高い類似性を示してしまう。
その問題に対して、より出現回数が少ないものが共起したときほど値が大きくなるように計算する手法がある。

それがPMI(Pointwise Mutual Information)。
日本語では自己相互情報量というらしい。

PMIの計算を普通に行うと共起数の少ないものが負の値になり、全く共起しないものが0になる。
これだと良くないのでPMIの負の値を全て0にしたものがPPMI(Positive Pointwise Mutual Information)

今回はPPMI計算用の関数を作成してPPMIの計算を行う。

import numpy as np

# 関数：PPMI計算
# pmi(X, i, j) = log( P(Xij) / P(Xi)・P(Xj) )
# 引数：df ⇒ 共起行列、上の式でいうところのP(Xij)
def calc_ppmi(df):
    # PMI の計算
    word_freq = df.sum(axis=0) # 各単語の出現回数の合計
    total_word_freq = word_freq.sum() # 全単語の出現回数の合計
    expected = np.outer(word_freq, word_freq) # 各単語の出現確率だけから推定した 単語A × 単語B の発生確率表
    df = (df * total_word_freq) / expected # 確率なので合計値(total)で割る、分母は2回、分子は1回割るから分子に1回かける
    with np.errstate(divide='ignore'): df = np.log(df) # 対数をとる　log(0)のエラーは無視して後で処理
    df[np.isinf(df)] = 0.0  # log(0)の結果である「-inf」を「0」とする
    # PPMI の計算　負の値を0にする
    df[df < 0] = 0.0
    return df
    
#### 3. PPMI
ppmi = calc_ppmi(co_occurrence)
ppmi.to_csv("yugioh_log_ppmi.csv", encoding="shift-jis")

こんな感じになる↓

商品	クリッター	サイクロン	ハリケーン	ブラック・ホール	ブラック・マジシャン	ブラック・マジシャン・ガール	リビングデッドの呼び声	大嵐	死のマジック・ボックス	死者蘇生	聖なるバリア −ミラーフォース−	融合	融合解除	青眼の白龍
クリッター	0.16	0.00	0.40	0.00	0.00	0.00	0.31	0.31	0.00	0.00	0.00	0.03	0.07	0.16
サイクロン	0.00	0.65	0.10	0.00	0.01	0.19	0.01	0.00	0.01	0.00	0.55	0.13	0.00	0.00
ハリケーン	0.40	0.10	1.34	0.00	0.00	0.00	0.56	1.25	0.00	0.00	0.00	0.27	0.00	0.00
ブラック・ホール	0.00	0.00	0.00	0.46	0.12	0.30	0.12	0.00	0.12	0.00	0.00	0.00	0.16	0.66
ブラック・マジシャン	0.00	0.01	0.00	0.12	1.16	0.65	0.00	0.00	1.16	0.00	0.31	0.00	0.00	0.00
ブラック・マジシャン・ガール	0.00	0.19	0.00	0.30	0.65	0.83	0.00	0.00	0.65	0.00	0.50	0.00	0.00	0.00
リビングデッドの呼び声	0.31	0.01	0.56	0.12	0.00	0.00	1.16	0.00	0.00	0.00	0.00	0.18	0.00	1.01
大嵐	0.31	0.00	1.25	0.00	0.00	0.00	0.00	1.85	0.00	0.35	0.00	0.18	0.51	0.00
死のマジック・ボックス	0.00	0.01	0.00	0.12	1.16	0.65	0.00	0.00	1.16	0.00	0.31	0.00	0.00	0.00
死者蘇生	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.35	0.00	0.23	0.20	0.06	0.11	0.20
聖なるバリア −ミラーフォース−	0.00	0.55	0.00	0.00	0.31	0.50	0.00	0.00	0.31	0.20	0.85	0.03	0.00	0.00
融合	0.03	0.13	0.27	0.00	0.00	0.00	0.18	0.18	0.00	0.06	0.03	0.12	0.00	0.03
融合解除	0.07	0.00	0.00	0.16	0.00	0.00	0.00	0.51	0.00	0.11	0.00	0.00	0.27	0.36
青眼の白龍	0.16	0.00	0.00	0.66	0.00	0.00	1.01	0.00	0.00	0.20	0.00	0.03	0.36	1.55

3.4. コサイン類似度の計算

PPMIの結果を利用して任意の商品同士の類似度を計算できる。
この商品を買った人はこの商品も買ってますみたいなやつ。
クラスタリングだけが目的ならこれはやる必要が無い。

コサイン類似度はscikitlearnにあるライブラリを使うことで表ごとまとめて計算してくれる。

それだと若干扱いづらいのでリストに変換して出力した。

#### 4. Cosine類似度
from sklearn.metrics.pairwise import cosine_similarity 
cos_sim_matrix = cosine_similarity(ppmi)
cos_sim_matrix = pd.DataFrame(data=cos_sim_matrix, index=ppmi.index, columns=ppmi.columns)

# Cosine類似度表csv出力
cos_sim_matrix.to_csv("yugioh_log_ppmi_cossim.csv", encoding="shift-jis")

# Cosine類似度リスト作成
import itertools
output_list = []
for combi in itertools.combinations(cos_sim_matrix.index, 2):
    output_list.append( [ combi[0], combi[1], cos_sim_matrix[combi[0]][combi[1]] ] )
    output_list.append( [ combi[1], combi[0], cos_sim_matrix[combi[0]][combi[1]] ] )

# Cosine類似度リストcsv出力
import csv
with open('yugioh_log_ppmi_cossim_list.csv', 'w', newline="") as f:
  writer = csv.writer(f)
  writer.writerow(["card A", "card B", "Cosine類似度"])
  writer.writerows(output_list)

コサイン類似度表(最大は1)↓

商品	クリッター	サイクロン	ハリケーン	ブラック・ホール	ブラック・マジシャン	ブラック・マジシャン・ガール	リビングデッドの呼び声	大嵐	死のマジック・ボックス	死者蘇生	聖なるバリア −ミラーフォース−	融合	融合解除	青眼の白龍
クリッター	1.00	0.08	0.92	0.27	0.00	0.00	0.74	0.78	0.00	0.45	0.00	0.87	0.54	0.48
サイクロン	0.08	1.00	0.13	0.08	0.20	0.46	0.06	0.07	0.20	0.25	0.85	0.38	0.00	0.01
ハリケーン	0.92	0.13	1.00	0.04	0.00	0.01	0.47	0.90	0.00	0.44	0.02	0.90	0.48	0.16
ブラック・ホール	0.27	0.08	0.04	1.00	0.33	0.44	0.57	0.04	0.33	0.32	0.20	0.10	0.56	0.83
ブラック・マジシャン	0.00	0.20	0.00	0.33	1.00	0.90	0.00	0.00	1.00	0.07	0.60	0.01	0.02	0.02
ブラック・マジシャン・ガール	0.00	0.46	0.01	0.44	0.90	1.00	0.02	0.00	0.90	0.14	0.79	0.06	0.05	0.07
リビングデッドの呼び声	0.74	0.06	0.47	0.57	0.00	0.02	1.00	0.21	0.00	0.24	0.00	0.60	0.34	0.85
大嵐	0.78	0.07	0.90	0.04	0.00	0.00	0.21	1.00	0.00	0.65	0.03	0.74	0.69	0.06
死のマジック・ボックス	0.00	0.20	0.00	0.33	1.00	0.90	0.00	0.00	1.00	0.07	0.60	0.01	0.02	0.02
死者蘇生	0.45	0.25	0.44	0.32	0.07	0.14	0.24	0.65	0.07	1.00	0.34	0.44	0.82	0.37
聖なるバリア −ミラーフォース−	0.00	0.85	0.02	0.20	0.60	0.79	0.00	0.03	0.60	0.34	1.00	0.21	0.02	0.02
融合	0.87	0.38	0.90	0.10	0.01	0.06	0.60	0.74	0.01	0.44	0.21	1.00	0.37	0.29
融合解除	0.54	0.00	0.48	0.56	0.02	0.05	0.34	0.69	0.02	0.82	0.02	0.37	1.00	0.55
青眼の白龍	0.48	0.01	0.16	0.83	0.02	0.07	0.85	0.06	0.02	0.37	0.02	0.29	0.55	1.00

コサイン類似度リスト(一部抜粋)↓

card A	card B	Cosine類似度
ブラック・マジシャン	死のマジック・ボックス	1
死のマジック・ボックス	ブラック・マジシャン	1
クリッター	ハリケーン	0.9234974389
ハリケーン	クリッター	0.9234974389
ブラック・マジシャン	ブラック・マジシャン・ガール	0.9029729248
ブラック・マジシャン・ガール	ブラック・マジシャン	0.9029729248
ブラック・マジシャン・ガール	死のマジック・ボックス	0.9029729248
死のマジック・ボックス	ブラック・マジシャン・ガール	0.9029729248
ハリケーン	融合	0.8996990148
融合	ハリケーン	0.8996990148
ハリケーン	大嵐	0.8973861356
大嵐	ハリケーン	0.8973861356
クリッター	融合	0.8687967339
融合	クリッター	0.8687967339
サイクロン	聖なるバリア −ミラーフォース−	0.8519482014
聖なるバリア −ミラーフォース−	サイクロン	0.8519482014
リビングデッドの呼び声	青眼の白龍	0.8489787168
青眼の白龍	リビングデッドの呼び声	0.8489787168
ブラック・ホール	青眼の白龍	0.8318634432

3.5. SVD

SVDという手法で次元削減を行う。
基本的に次元数が多いと特徴が捉えづらく分析に不向き。

今回の例では商品数が14と少ないので必要ないが次元数が多い時は有効。
本当は1000次元から100次元にしたりとがっつり削減する。

#### 5. SVD
from sklearn.decomposition import TruncatedSVD
svd = TruncatedSVD(n_components=5) # 目標の次元数　5
svd_array = svd.fit_transform(ppmi)
svd_df = pd.DataFrame(data=svd_array, index=ppmi.index, columns=list(range(5)), dtype='float') # columnsの定数はさっきの次元数

3.6. クラスタリング

クラスタリングは前回やったので説明しない。

#### 6. クラスタリング(SpectralClustering)
from sklearn import cluster
from scipy.sparse import csr_matrix

# クラスタリング実行
csr = csr_matrix(svd_df) # スパースマトリクスに変換
spectral_clustering = cluster.SpectralClustering(n_clusters=5, affinity='nearest_neighbors', n_init=100, assign_labels='discretize')
predict_s = spectral_clustering.fit_predict(csr)

# クラスタリング結果csv出力
result = pd.DataFrame({"class Spectral":predict_s}, index=svd_df.index)
result.to_csv("yugioh_log_ppmi_svd_class.csv", encoding="utf-8")

クラスタリングの結果↓

商品	class
クリッター	0
サイクロン	2
ハリケーン	4
ブラック・ホール	3
ブラック・マジシャン	3
ブラック・マジシャン・ガール	3
リビングデッドの呼び声	4
大嵐	1
死のマジック・ボックス	2
死者蘇生	0
聖なるバリア −ミラーフォース−	2
融合	0
融合解除	1
青眼の白龍	1

3.7. 結果

それらしい結果は出た。
ちゃんと動いている。

PPMIによって出現頻度の大小に関わらず類似度を計算できるようにしたが、そもそも出現頻度に大きな偏りがない。
共起行列・SVDによって次元数の削減を目論んだが、そもそも次元数が小さい。

多分もっと大きなデータで実験したら差が出てくる。

4. コード

全部まとまった状態のコード

import pandas as pd
import numpy as np

# 関数：PPMI計算
# pmi(X, i, j) = log( P(Xij) / P(Xi)・P(Xj) )
# 引数：df ⇒ 共起行列、上の式でいうところのP(Xij)
def calc_ppmi(df):
    # PMI の計算
    word_freq = df.sum(axis=0) # 各単語の出現回数の合計
    total_word_freq = word_freq.sum() # 全単語の出現回数の合計
    expected = np.outer(word_freq, word_freq) # 各単語の出現確率だけから推定した 単語A × 単語B の発生確率表
    df = (df * total_word_freq) / expected # 確率なので合計値(total)で割る、分母は2回、分子は1回割るから分子に1回かける
    with np.errstate(divide='ignore'): df = np.log(df) # 対数をとる　log(0)のエラーは無視して後で処理
    df[np.isinf(df)] = 0.0  # log(0)の結果である「-inf」を「0」とする
    # PPMI の計算　負の値を0にする
    df[df < 0] = 0.0
    return df

#### CSV読み込み
loadcsv = "yugioh_log.csv"
df = pd.read_csv(loadcsv, encoding="shift-jis") # ← CSVの文字コードがutf8なら encoding="utf-8"

#### 1. クロス集計
cross = pd.crosstab(df["商品"], df["購入者"])
cross = cross.mask(cross > 0, 1) # 2回以上でも1にする

#### 2. 共起行列
co_occurrence = cross.dot(cross.T)
co_occurrence.to_csv("yugioh_log_co_occurrence.csv", encoding="shift-jis")

#### 3. PPMI
ppmi = calc_ppmi(co_occurrence)
ppmi.to_csv("yugioh_log_ppmi.csv", encoding="shift-jis")

#### 4. Cosine類似度
from sklearn.metrics.pairwise import cosine_similarity 
cos_sim_matrix = cosine_similarity(ppmi)
cos_sim_matrix = pd.DataFrame(data=cos_sim_matrix, index=ppmi.index, columns=ppmi.columns)

# Cosine類似度表csv出力
cos_sim_matrix.to_csv("yugioh_log_ppmi_cossim.csv", encoding="shift-jis")

# Cosine類似度リスト作成
import itertools
output_list = []
for combi in itertools.combinations(cos_sim_matrix.index, 2):
    output_list.append( [ combi[0], combi[1], cos_sim_matrix[combi[0]][combi[1]] ] )
    output_list.append( [ combi[1], combi[0], cos_sim_matrix[combi[0]][combi[1]] ] )

# Cosine類似度リストcsv出力
import csv
with open('yugioh_log_ppmi_cossim_list.csv', 'w', newline="") as f:
  writer = csv.writer(f)
  writer.writerow(["card A", "card B", "Cosine類似度"])
  writer.writerows(output_list)

#### 5. SVD
from sklearn.decomposition import TruncatedSVD
svd = TruncatedSVD(n_components=5) # 元の次元数が少ないから5にしてるけど本当は1000次元から100次元に削減したりする
svd_array = svd.fit_transform(ppmi)
svd_df = pd.DataFrame(data=svd_array, index=ppmi.index, columns=list(range(5)), dtype='float') # columnsの定数はさっきの次元数

#### 6. クラスタリング(SpectralClustering)
from sklearn import cluster
from scipy.sparse import csr_matrix

# クラスタリング実行
csr = csr_matrix(svd_df) # スパースマトリクスに変換
spectral_clustering = cluster.SpectralClustering(n_clusters=5, affinity='nearest_neighbors', n_init=100, assign_labels='discretize')
predict_s = spectral_clustering.fit_predict(csr)

# クラスタリング結果csv出力
result = pd.DataFrame({"class Spectral":predict_s}, index=svd_df.index)
result.to_csv("yugioh_log_ppmi_svd_class.csv", encoding="utf-8")

5. 参考

PPMIの計算方法について
https://stackoverflow.com/questions/58701337/how-to-construct-ppmi-matrix-from-a-text-corpus

タグ Machine Learning, Python, pandas, scikit-learn

商品購入ログから商品間の類似度取得・クラスタリング

1. 環境構築

2. 使用データ

3. 実験

3.1. クロス集計

3.2. 共起行列　作成

3.3. PPMI 計算

3.4. コサイン類似度の計算

3.5. SVD

3.6. クラスタリング

3.7. 結果

4. コード

5. 参考

関連する記事

タグクラウド

最近の記事

アーカイブ

タグ

スポンサー

最近の記事

アーカイブ

タグ

スポンサー

Your browser is out-of-date!

商品購入ログから商品間の類似度取得・クラスタリング

1. 環境構築

2. 使用データ

3. 実験

3.1. クロス集計

3.2. 共起行列 作成

3.3. PPMI 計算

3.4. コサイン類似度の計算

3.5. SVD

3.6. クラスタリング

3.7. 結果

4. コード

5. 参考

関連する記事

タグクラウド

最近の記事

アーカイブ

タグ

スポンサー

最近の記事

アーカイブ

タグ

スポンサー

Your browser is out-of-date!

3.2. 共起行列　作成